Form Factor calculation with the Material Class¶

Note: This module is still a work-in-progress and the usage of these classes and/or functions may change in the future.

The following are examples on the usage of the Material class, used to define a material and calculate the structural form factor in reciprocal lattice units for a given \(q\). This tutorial will cover the utilization of this class and its methods.

Defining the Material¶

For this example we will use Fe_1.1Te, a high-temperature tetragonal \(P4/nmm\) structure with Fe in the 2a positions, Te in the 2c positions, and excess Fe in the interstitial 2c positions. First we build the dictionary defining the material to pass it to the class:

def_FeTe = {'name': 'Fe1.1Te',
            'composition': [{'ion': 'Fe', 'pos': [0.75, 0.25, 0.0]},
                            {'ion': 'Fe', 'pos': [0.25, 0.75, 0.0]},
                            {'ion': 'Te', 'pos': [0.25, 0.25, 0.2839]},
                            {'ion': 'Te', 'pos': [0.75, 0.75, -0.2839]},
                            {'ion': 'Fe', 'pos': [0.25, 0.25, 0.721], 'occupancy': 0.1},
                            {'ion': 'Fe', 'pos': [0.75, 0.75, -0.721], 'occupancy': 0.1}],
            'debye-waller': False,
            'massNorm': False,
            'lattice': {'abc': [3.81, 3.81, 6.25],
                        'abg': [90, 90, 90]},
           }

Note

The 'massNorm' key should be set to False to return the structure factor in units of barns. 'massNorm' is used for calculation of the coherent one-phonon inelastic cross-section, which depends on a calculation of nuclear structure factor in which the coherent scattering lengths are normalized by the square-root of the atomic mass i.e. \(\bar{b}_d/\sqrt{M_d}\) (see Eq. 4.88 in “Theory of neutron scattering from condensed matter, Volume 1” by Stephen W. Lovesey.

Initializing the Material class¶

Once we have built our material in the above format we can initialize the class.

>>> from neutronpy import Material
>>> FeTe = Material(def_FeTe)

Calculating the structure factor¶

Note

The structure factor calculation method calc_nuc_str_fac returns the full structure factor term \(F(q)\), including any imaginary parts, and not \(\left|F(q)\right|^2\) which is typically used in other calculations.

Now that our material is defined, we can calculate the structural form factor with calc_nuc_str_fac. First, we will calculate it at a single point \(q\):

>>> str_fac = FeTe.calc_nuc_str_fac((1, 1, 0))

We can also calculate the structure factor over a range of values in a similar way. In this example we are calculating the structure factor in the (h, k, 0) plane where \(0 < h,k < 2\), with a step size of 0.025 r.l.u.

>>> import numpy as np
>>> h, k = np.meshgrid(np.linspace(0, 1, 41), np.linspace(0, 1, 41), sparse=True)
>>> str_fac = FeTe.calc_nuc_str_fac((h, k, 0))

The resulting plot of this structure factor would look like the following figure.

(Source code, png, hires.png, pdf)

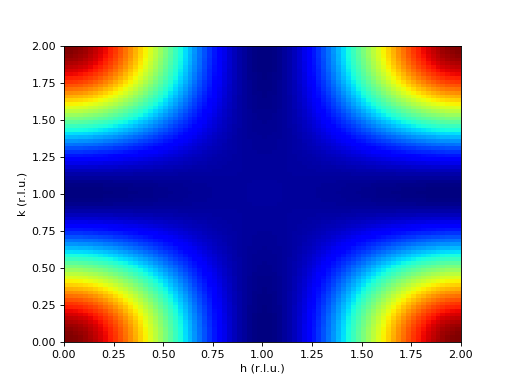
Note

The above picture will only be reproducible if the structure factor is partially symmetrized, i.e. in this case the calculation would be:

str_fac = 0.25 * (np.abs(FeTe.calc_nuc_str_fac((h, k, 0))) ** 2 +
                  np.abs(FeTe.calc_nuc_str_fac((-h, k, 0))) ** 2 +
                  np.abs(FeTe.calc_nuc_str_fac((h, -k, 0))) ** 2 +
                  np.abs(FeTe.calc_nuc_str_fac((-h, -k, 0))) ** 2)

Using space group to properly symmetrize¶

By providing a space group symbol or number in the following way it is possible to automatically symmetrize a crystal structure.

>>> def_FeTe['space_group'] = 'P4/nmm'
>>> FeTe = Material(def_FeTe)

Calculating the resulting Material object’s structure factor as in the previous example would result in the following figure, where the crystal structure is fully symmetrized.

(Source code, png, hires.png, pdf)

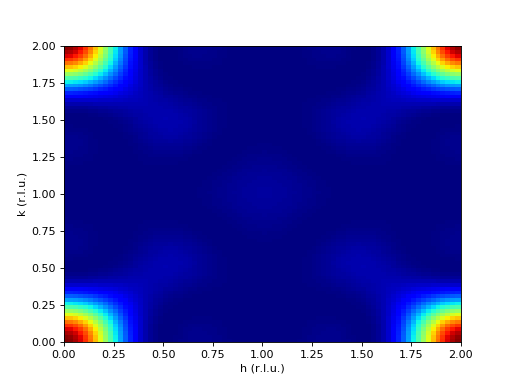
Warning

This feature is currently broken in the sense the absolute values are incorrect due to a bug in the symmetrization routine.